Площа рівнобедреного трикутника формула

У даній статті мова піде про те як знайти площу рівнобедреного трикутника і формули для вирішення.
Трикутник це такий трикутник у якого дві паралельні основі сторони рівні. Він зображений на малюнку.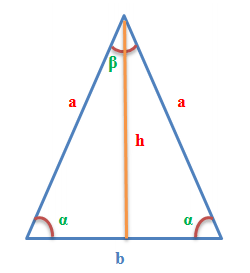

Варто зауважити що букви якими позначені сторони і кути, використовуються в формулах, для вашої зручності.
Замітка: Якщо вам потрібна якісно виконана курсова або контрольна робота, без посередників. Тоді Вам на сайт tvoi5.ru. Так само Ви можете перейти по посиланню курсова на замовлення ( http://tvoi5.ru/zakazat-kursovuyu-rabotu.html ) І всі подробиці.

Площа рівнобедреного трикутника формула.

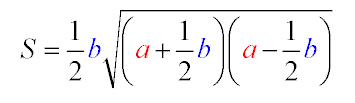
Перша формула говорить про те що площа знаходиться, якщо нам відома тільки одна сторона і основа трикутника. Отримали цю формула за допомогою використання загальної формули. Коли основним є формула Герона і сторони фігури рівні, вона сама по собі буде виглядати простіше.

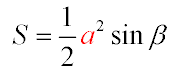
У другій формулі говориться про те що площа знаходиться через бічні сторони і кут знаходиться між ними. Або sin кута знаходиться між бічних сторін, помножений на половину квадрата однієї з бічних сторін. Коли проводимо висоту на бічній стороні її довжина дорівнює а * sin ?. Так як довжину сторони ми знаємо, то і її висота нам відома. Відповідно, площа рівнобедреного трикутника буде половина від їх вираження. Якщо точніше. то ціла величина робить площа трикутника. Поділяючи висотою прямокутник, отримуємо два не великих прямокутних трикутника. Діагоналлю буде сторона трикутника, в свою чергу вона ділить фігуру на дві рівні частини. З чого випливає що шукана нами величина знаходиться як половина величини одного боку умножаемая на висоту.

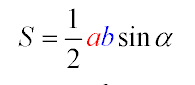
У третій формулою площа знаходиться за допомогою однієї паралельної боку, підстави і кута знаходиться на вершині. Іншими словами можна сказати так: коли відомий хоч один кут в трикутник, з його допомогою можна дізнатися і два інших. Дана формула схожа з другої формулою, можна використовувати і запам'ятати будь-яку з них. Але з цієї формули вийде п'ята, яку опишу трохи нижче.

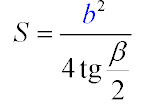
Четверта формула показує що знайти площу можна знаючи величину підстави і кута при ньому. Всі кути біля основи однакові і квадрат сторони підстави розділений на 4 tg підлогу кута, що з'явилися від його бічних сторін. Коли уважно розглядати, можна зрозуміти, підлогу боку підстави b / 2, при множенні tg (? / 2) дає висоту. Яка в свою чергу грає роль медіани і бісектриси, а значить tg (? / 2) = (b / 2) / h, з чого h = b / (2tg (? / 2)) і зводитися до спрощеної формулою №5.

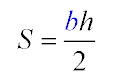
Отже п'ята формула вона говорить про те, що знайти площу можна за допомогою висоти яка бере початок в вершині трикутника і закінчується в його підставі, при цьому розділяючи його на прямокутні трикутники. А далі як в третій і четвертій формулах. Пол величини висоти помножене на величину підстави.

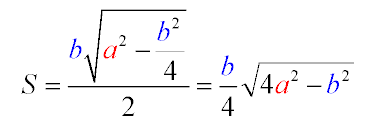
Шоста і остання формула. Вона з'являється в ході рішення площі трикутника через теорему Піфагора. Нам знадобитися висота, знайдена в минулому формулою. Вона так само доводиться катетом від прямокутного трикутника, отриманого від бічної сторони, половини підстави плюс висота. Гіпотенузою буде бічна сторона, з квадрата гіпотенузи (а) віднімемо другий катет в квадраті. Так як він дорівнює підлозі - підстави (b / 2) означає квадрат = b2 / 4. Витягуючи корінь з отриманого, знайдемо висоту.