Better Explained: дивовижні застосування теореми Піфагора

1. Йдемо до розуміння площі
2. А можна взяти взагалі будь-лінійний сегмент?
3. А можна взяти взагалі будь-яку геометричну фігуру?
4. Інтуїтивне розуміння теореми Піфагора
5. Застосування теореми: Візьмемо будь-яку фігуру
6. Застосування теореми: збереження квадратів
7. Спробуйте самі
8. Насолоджуйтесь

Теорема Піфагора - справжня знаменитість в світі математики: вже якщо її формула засвітилася в серіалі «Сімпсони», вона точно відома всім.

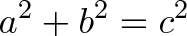
Більшість вважає, що формула теореми Піфагора може бути застосована тільки в геометрії і тільки до трикутниках. Швидше за все, при згадці цієї теореми ви згадуєте щось таке:

джерело: вікіпедія

А тепер вдумайтеся: теорема Піфагора працює для будь-яких фігур і для всіх квадратних рівнянь.

Якщо ви продовжите читати статтю, ви дізнаєтеся, як ця теорема віком в 2,5 тисячі років може допомогти нам розібратися в інформаційних технологіях, фізики і навіть в повній мірі оцінити силу соціальних мереж.

Йдемо до розуміння площі

Завжди цікаво подивитися на звичне під новим кутом. Наприклад, до написання цієї статті я ніколи не замислювався про глибинний понятті такого явища, як «площа фігури». Так, ми можемо пам'ятати формули, але ось чи розуміємо ми саму природу площі?

Дивно, але площа будь-якої фігури може бути обчислена шляхом зведення в квадрат будь-якого лінійного сегмента. Лінійний сегмент - це відрізок прямої, який ми вибираємо в геометричній фігурі. Наприклад, в якості лінійного сегмента квадрата ми вибрали сторону. Тоді площею квадрата є квадрат його боку (сторона = 5, площа = 25). Як лінійного сегмента кола можна взяти радіус, і тоді площею кола буде число π, помножене на квадрат його радіуса (радіус = 5, площа = 25π). Куди простіше?

Ми можемо взяти будь-який лінійний сегмент і з його допомогою обчислити площу: кожен лінійний сегмент, зведений в квадрат, дасть нам величину площі фігури, якщо його помножити на певний коефіцієнт. Так ми отримуємо універсальну формулу розрахунку площі фігури:

Площа фігури = Коефіцієнт * (лінійний сегмент) ²

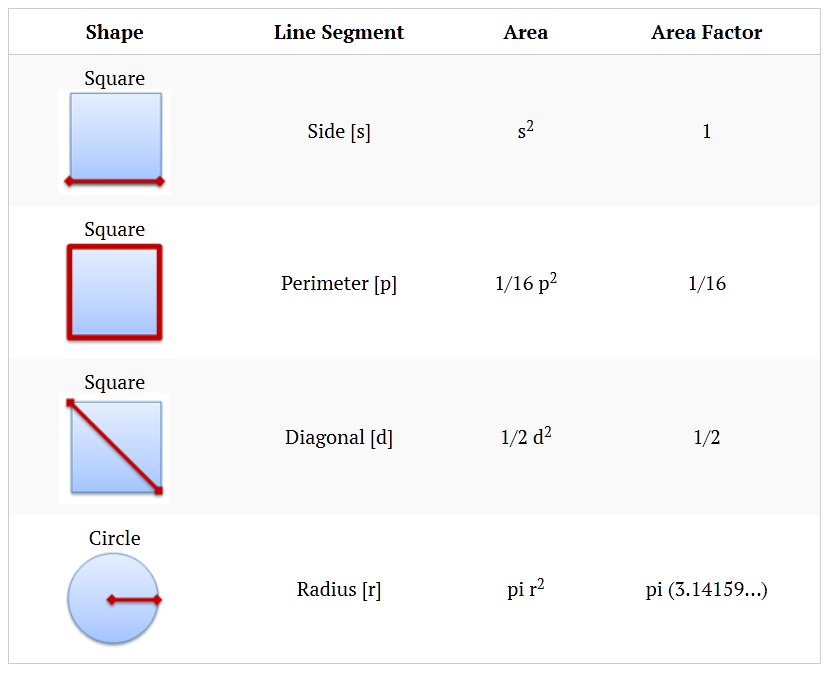
Подивіться на діагональ d квадрата. Сторона квадрата при цьому буде обчислюватися як d, поділена на √2. У цьому випадку площа квадрата буде обчислюватися як 1/2 d². Якщо ми хочемо використовувати діагональ фігури в якості лінійного сегмента, нашим коефіцієнтом буде число 1/2.

А тепер як лінійного сегмента використовуємо периметр p. Сторона квадрата - це p / 4, значить, його площа обчислюється за формулою p² / 16. В цьому випадку коефіцієнтом для p² буде 1/16.

А можна взяти взагалі будь-лінійний сегмент?

А як же! Між «традиційним» сегментом (ну, наприклад, стороною квадрата) і будь-яким іншим на ваш смак (скажімо, периметром) завжди існує взаємозв'язок (нескладно здогадатися, що периметр буде дорівнює чотирьом сторонам квадрата). Якщо ми можемо конвертувати новий сегмент в традиційний, площа обчислюється легко - зміниться лише коефіцієнт в рівнянні.

А можна взяти взагалі будь-яку геометричну фігуру?

Майже. Універсальна формула працює для всіх подібних фігур - тих, що є збільшеними або зменшеними версіями однієї і тієї ж фігури. Ну наприклад:

Всі квадрати схожі один на одного (площа квадрата - завжди квадрат однієї його сторони). Всі кола схожі один на одного (площа кола - завжди π * r²). Трикутники не схожі один на одного: вони бувають витягнутими або плоскими, «толстенькими» і «тоненькими», і у кожного трикутника - свій коефіцієнт для обчислення площі в залежності від того, який лінійний сегмент ви вибрали. Змініть форму трикутника, зміниться і рівняння.

В цілому все трикутники підкоряються правилу «площа = 1/2 підстави * висоту». Але відносини між підставою і висотою залежать від виду трикутника, тому і коефіцієнт в універсальній формулі буде завжди різним.

Чому для збереження універсальності рівняння необхідні подібні фігури? Інтуїтивно зрозуміло, що при масштабуванні фігури ви міняєте її розмір, але зберігаєте пропорції. Периметр квадрата завжди буде обчислюватися множенням розміру його боку на 4.

Оскільки коефіцієнт у формулі площі грунтується на відносинах між елементами фігури, формула буде працювати для всіх фігур з однаковими пропорціями (подібними фігурами). Це як сказати, що повний розмах рук людини приблизно відповідає його росту - незалежно від того, хто перед нами, дитина або баскетболіст.

джерело: вікіпедія

Так ось, основна концепція розрахунку площі фігури може бути виражена в наступних трьох постулатах:

• Площа фігури обчислюється за допомогою зведення в квадрат будь-якого її лінійного сегмента.
• У кожного лінійного сегмента буде свій коефіцієнт в універсальній формулі.
• Одна і та ж формула розрахунку площі працює для всіх подібних фігур.

Інтуїтивне розуміння теореми Піфагора

Ніхто не сперечається з тим, що теорема Піфагора працює. Але майже всі її докази засновані на механічних діях: переставляємо місцями фігури, і вуаля! - рівняння все одно працює. Давайте подумаємо: вам правда інтуїтивно зрозуміло, що рівняння має виглядати як a² + b² = c²? А чому не 2a² + b² = c²? Давайте спробуємо знайти в цьому сенс.

Для початку нам знадобиться усвідомити і прийняти дивовижний факт: будь-який прямокутний трикутник можна розбити на два подібних прямокутних трикутника.

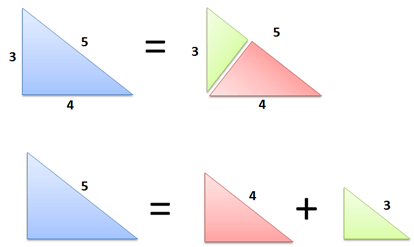
Круто так? Всього один опущений перпендикуляр, і один трикутник перетворюється в дві свої маленькі копії.

Власне, цей приклад говорить нам про дуже просту річ:

Площа (чогось великого) = Площа (дечого середнього) + площа (дечого поменше)

Маленькі трикутники були отримані з великого, тому ми просто складаємо їх площі. І так, найголовніше: оскільки трикутники подібні, для них діє одна і та ж формула обчислення площі.

Давайте назвемо довгу сторону (з довжиною 5) - с, середню сторону (з довжиною 4) - b, і коротку сторону (з довжиною 3) - a. Формула площі для цих трикутників виглядає так:

Площа = F * гіпотенуза²,

де F - це множник (в цьому випадку - 6/25 або 0,24). З формулою можна пограти:

Площа (чогось великого) = Площа (дечого середнього) + площа (дечого поменше)

Fc² = Fb² + Fa²

Просто приберіть F, і ви отримаєте:

c² = b² + a²

Ой, так це ж наша улюблена теорема! Ми знали, що вона нас не підведе, але тепер ми розуміємо, чому:

• Трикутник можна розбити на два маленьких подібних трикутника
• Оскільки площі малих трикутників складаються, квадрати гіпотенуз також складаються.

Звичайно, теорема Піфагора працює тільки в Евклідовій геометрії і не може застосовуватися, наприклад, до сфер. Але про це потрібно поговорити іншим разом.

Застосування теореми: Візьмемо будь-яку фігуру

Раніше ми використовували просту плоску фігуру - трикутник. Але ж лінійний сегмент можна витягати з абсолютно будь-якої фігури. Візьмемо, наприклад, коло. На зображенні ми бачимо три різних кола з радіусами, рівними сторонам нашого піфагоровского трикутника.

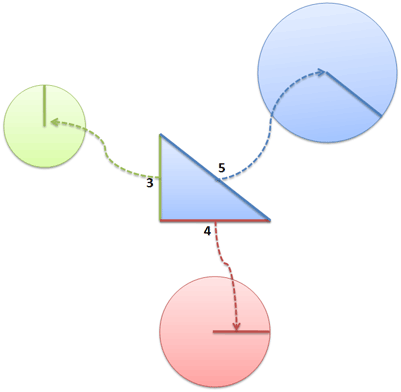
Чи можна з великим колом вчинити так само, як ми вчинили з великим трикутником - скласти площі менших кіл? При цьому ми будемо пам'ятати, що площа кожного маленького кола ми можемо вирахувати, використовуючи квадрат відомого нам лінійного сегмента, помножений на конкретний коефіцієнт - в даному випадку це буде число Пі.

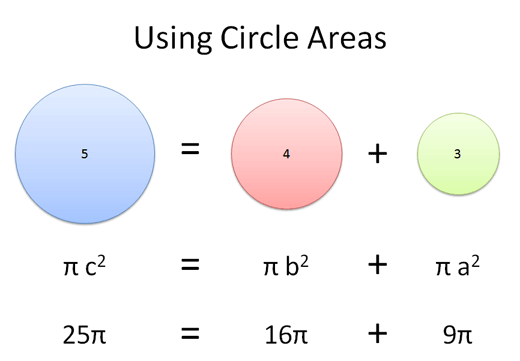
Так-так, все вірно: Площа кола радіусом 5 = Площа кола радіусом 4 + Площа кола радіусом 3.

Ми запросто підставляємо в формулу потрібний коефіцієнт, і вона все ще працює.

Пам'ятайте, що в якості лінійного сегмента може виступати будь-який елемент плоскої фігури. Ви могли вибрати радіус, діаметр або довжину окружності - змінився б тільки коефіцієнт, але відносини 3-4-5 залишилися б незмінними.

Теорема Піфагора дозволяє знаходити співвідношення площ будь-яких подібних фігур. Це те, чого нас не вчать в школі.

Застосування теореми: збереження квадратів

Теорема Піфагора застосовується до будь-якого квадратного рівняння. Подібно до того, як ви розбиваєте трикутники, ви можете розбити квадрат будь-якої кількості чого завгодно (c²) на менші його частки (a² + b²). Цим «чим завгодно» може бути відстань, енергія, людино-годин, час або кількість користувачів в соціальній мережі.

Соціальні мережі.

Є такий закон - закон Меткалфа , Який формулює рівень корисності соціальної мережі: він говорить, що цінність соціальної мережі зростає в квадратичної залежності від кількості користувачів в ній. наприклад:

Мережа з 50 млн. Користувачів = Мережа з 40 млн. Користувачів + Мережа з 30 млн. Користувачів

Здається дивним, що корисність соціальної мережі в 50 мільйонів чоловік виражається через корисність двох соцмереж, в сумі мають 70 мільйонів чоловік, але це насправді так. Соціальна мережа росте нелінійно.

Інформаційні технології.

Деяким програмам потрібно n² часу для обробки n запитів. Іншими словами:

50 запитів = 40 запитів + ​​30 запитів

Дивно, але 70 елементів даних, розбиті на дві групи, будуть оброблені так само швидко, як одна група з 50 елементів. Саме тому має сенс сортувати елементи по групах і підгрупах. Ця особливість використовується майже у всіх алгоритмах сортування. Теорема Піфагора допомагає зрозуміти, чому сортування 50 елементів відразу менш ефективна, ніж сортування цього ж кількості елементів окремо.

Площа поверхні.

Площа поверхні сфери визначається як 4πr². Що це означає?

Площа радіусом 50 = площу радіусом 40 + площу радіусом 30

У житті нам зустрічається не так вже й багато сфер, але ось портовим працівникам це знання дуже корисно (в кінці кінців, корпус будь-якого судна - це деформована сфера). Кількістю фарби, необхідної для 50-тіфутовой яхти, можна забарвити дві яхти довжиною 40 і 30 футів.

Фізика.

Якщо згадати шкільні уроки фізики, можна привести в приклад формулу розрахунку кінетичної енергії об'єкта масою m при швидкості v: 1 / 2mv². Застосовуємо теорему Піфагора.

Енергія при швидкості в 500 км / ч = Енергія при швидкості в 400 км / ч + Енергія при швидкості в 300 км / ч

Значить, одного і того ж кількості енергії вистачає або на запуск одного предмета на швидкості 500 км / год, або на запуск двох інших на меншій швидкості.

Спробуйте самі

У теорему Піфагора можна підставляти абсолютно будь-які цифри. Вона може допомогти нам і в повсякденному житті. Наприклад, ми ніяк не можемо вибрати: замовити велику піцу діаметром 50 см або дві діаметром 30 см? Ми з теоремою вже знайомі добре і нас не обдурити: площа однієї піци в 50 см буде дійсно більше, ніж площа двох піц по 30 см в діаметрі (можете перевірити, ми не обманюємо). Завжди можна підставити інші цифри, а для ледачих є простий і зручний калькулятор .

Насолоджуйтесь

Зі шкільної лави ми впевнені, що теорема Піфагора - це щось про трикутниках і геометрії. Ми з вами разом переконалися, що це не так.

Пам'ятайте, що сторони прямокутного трикутника можуть перетворитися в лінійний сегмент будь-якої фігури, і стати змінними в будь-якому квадратному рівнянні. І це приголомшливо.

Дякую чудовій статті на BetterExplained .

Знайшли друкарську помилку? Виділіть фрагмент і натисніть Ctrl + Enter.