Лекція № 11. Перетин поверхні тіл обертання проецирующей площиною

Лекція № 11. Перетин поверхні тіл обертання проецирующей площиною

1. Перетин поверхні циліндра

Бувають такі випадки перетину поверхні прямого кругового циліндра площиною:

1) окружність, якщо січна площина Р перпендикулярна осі циліндра, причому вона паралельна основі циліндра (рис. 104а);

2) еліпс, якщо січна площина Р НЕ перпендикулярна і не паралельна осі циліндра (рис. 104б);

3) пара прямих, якщо січна площина Q містить вісь циліндра або паралельна їй (рис. 104В).

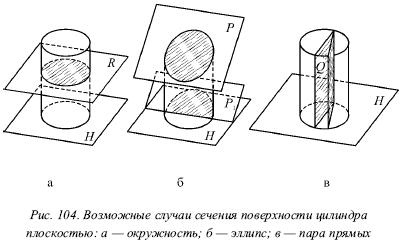
Особливий інтерес представляє випадок, коли похила січна площина перетинає основу циліндра (площину Р 1 на рис. 104б). Тут частина еліпса може бути невірно прийнята за параболу або гіперболу. Потрібно знати, що ні парабола, ні гіпербола не можуть бути отримані як перетин поверхні кругового циліндра площиною.

На малюнку 105 показано перетин поверхні циліндра фронтально-проектує площиною Р. Тут для циліндра розглянуто рішення всіх трьох основних завдань, пов'язаних з перетином тіла площиною, т. Е. Відшукання проекцій перетину, його натуральний вигляд і побудова розгортки.

Проекції перетину. На малюнку 105а розглянуто наочне зображення перетину, а звідси видно, що велика вісь еліпса представлена хордою 0-6, яка перетинає вісь циліндра в точці С. При цьому мала вісь направлена по горизонталі, перпендикулярної в площині V. Отже, мала вісь проектується без спотворення на горизонтальній і профільної площини (рис. 105б), а центр еліпса знаходиться на осі циліндра (точка С). Слід зазначити, що на малюнку 105б вісь симетрії проходить через точки 0-6.

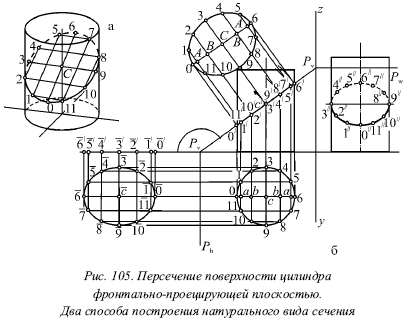
Добутий в горизонтальному перетині еліпс проектується на площину у вигляді кола основи, а на профільну площину - у вигляді еліпса. При цьому велика вісь еліпса 3? -9? �� проекцією малої осі 3-9 вихідного еліпса, а мала вісь 0? -6? є проекцією великий осі 0-6. На фронтальній площині проекція еліпса є відрізок 0? -6 ?, який дорівнює великої осі самого еліпса.

Отже, на самому початку побудови можна отримати дві готові проекції перетину: горизонтальну і фронтальну. Після цього потрібно побудувати тільки профільну проекцію. Слід зауважити, що точки 3? �� 9? відокремлюють видиму частину кривої від невидимої на профільній проекції. Якщо січна площина Р нахилена до площини основи циліндра під кутом 45 °, то профільна проекція еліпса є колом. На малюнку 105 кут нахилу січної площини менше 45 °, внаслідок цього профільна проекція великий осі представляє собою малу вісь профільної проекції еліпса. У тому випадку, якщо б кут нахилу січної площини був більше 45 °, проекція великий осі була б великою віссю профільної проекції еліпса.

Побудова натуральний вигляд перерізу. Спочатку потрібно зазначити цифрами ряд точок на проекціях еліпса (на рис. 105 зазначено 12 таких точок), після чого слід починати побудову натуральний вигляд перерізу. Виконати це можна двома способами:

1) побудовою суміщення площині Р з горизонтальною площиною шляхом обертання її близько горизонтального сліду P h. На малюнку 105 суміщення побудовано зліва від P h і відповідні точки відзначені цифрами з межею зверху;

2) вказівкою 12 точок еліпса. При цьому хорди, паралельні P h, проектуються без спотворення на горизонтальну площину, а відстані між цими хордами проектуються на фронтальну площину. Внаслідок цього проводять через точки сліду P v, які відзначені цифрами, прямі, перпендикулярні P v. Потім перпендикулярно цих лініях проводять вісь симетрії даного еліпса. Разом з крайніми допоміжними прямими її перетин визначить точки еліпса 0 і 6, т. Е. Кінці великої осі. Після цього від точок А, В і С слід відкласти в обидві сторони половини відповідних хорд (Al = а1, В2 = b 2, C 3 = з 3).

В даному випадку хорда 3-9 є малою віссю еліпса.

Розгортка. На малюнку 106 показано побудову розгортки бічної поверхні неусеченного циліндра. Ця бокова поверхня в розгорнутому стані є прямокутником, основа якого дорівнює довжині окружності (? D), а висота - утворює циліндра.

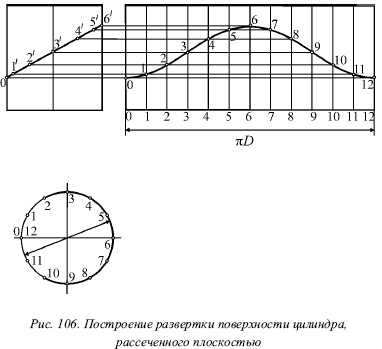
В даному випадку довжина кола замінена периметром вписаного правильного 12-кутника (рис. 106), після чого через відповідні точки поділів спрямленной окружності проведені утворюють. При цьому на кожній утворює відзначена її точка зустрічі з площиною Р.

2. Перетин поверхні конуса

У загальному випадку кругова конічна поверхня включає в себе дві абсолютно однакові порожнини, які мають загальну вершину (рис. 107В). Утворюють однієї порожнини представляють собою продовження утворюють інший порожнини. На практиці ми маємо справу не з нескінченно розширюються двома порожнинами конічної поверхні, а з тілом, яке обмежене однією порожниною цієї поверхні і площиною, що є звичайним круговим конусом.

Бувають різні випадки перетину поверхні кругового конуса площиною.

1. Еліпс, якщо січна площина не паралельна жодної утворює (рис. 107б). Тут січна площина перетинає поверхню тільки однієї порожнини конуса. Кут нахилу січної площини по відношенню до основи конуса менше кута, який утворює конуса становить з підставою конуса (рис. 108б). Тут кут є кутом, який утворює становить з підставою.

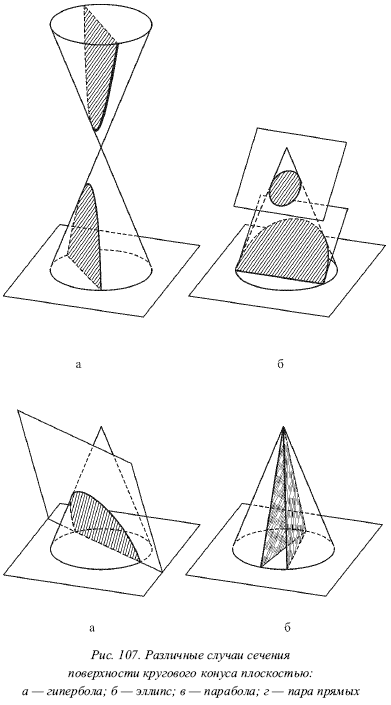
У тому випадку, якщо січна площина перпендикулярна осі конуса (? =?), Окружність можна розглядати як окремий випадок еліпса.

2. Парабола, якщо січна площина паралельна тільки одній що утворює (рис. 107В). Тут січна площина перетинає другу порожнини конуса, а кут нахилу v1? січної площини по відношенню до основи конуса дорівнює куту (рис. 108в).

На малюнку 108в площину Q паралельна утворює SA, а вісь параболи паралельна цій утворює.

3. Гіпербола, якщо січна площина паралельна двом утворюючим (рис. 107а). При цьому січна площина перетинає обидві порожнини конуса. Кут нахилу січної площини по відношенню до основи конуса більше кута (рис. 108а). На цьому малюнку для вказівки двох складових, яким паралельна січна площина R, потрібно провести через вершину конуса площину R 1, яка паралельна площині R. Площина R 1 повинна перетнути поверхню конуса по утворюючим SA і SB, яким буде паралельна площина R.

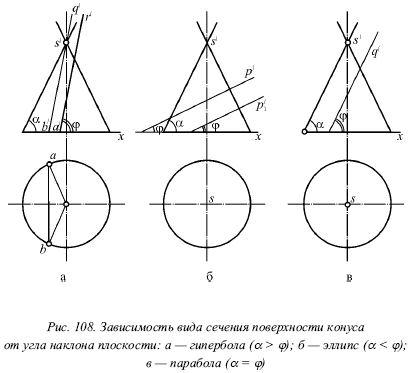
Зауважимо, що лише в разі гіперболи січна площина буде перетинати обидві порожнини конуса. Значить будь-яка площина, яка перетинає обидві порожнини конуса, обов'язково буде перетинати його поверхню по гіперболі.

4. Пара прямих, якщо січна площина проходить через вершину конуса і кут її нахилу до основи конуса більше кута (рис. 107 г). Цей випадок іноді розглядають як окремий випадок гіперболи.

Аналізуючи малюнок 108, зауважимо, що фронтально-проектує площину може давати перетину всіх розглянутих вище видів.

3. Перетин поверхні кулі

Будь-яке перетин поверхні кулі площиною є колом, яка проектується без спотворення тільки в тому випадку, якщо січна площина паралельна площині проекцій. У загальному ж випадку ми будемо отримувати еліпс. У тому випадку, якщо січна площина перпендикулярна площині проекцій, на цій площині проекцією кола є відрізок прямої, який дорівнює діаметру цієї окружності.

На малюнку 109 показано перетин поверхні кулі горизонтально-яка проектує площиною Р. На горизонтальну площину перетин буде проектуватися у вигляді відрізка проекції р площині Р, який укладений між контуром кулі і дорівнює діаметру окружності перетину. На фронтальній площині ми отримаємо еліпс. Про 1 є центром кола, який отриманий в перерізі кулі. Він розташований на одній висоті з центром кулі Про. Горизонтальна проекція про 1 центру О1 кола розташовується посередині відрізка ab. Перпендикуляр, який опущений з точки про на пряму ab, потрапляє в точку про 1, що є горизонтальною проекцією центру кола перетину. Фронтальна проекція о? 1центра кола є центром цікавить нас еліпса.

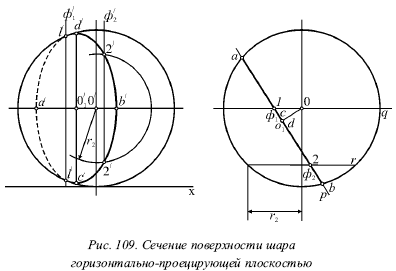
Якщо розглядати еліпс як проекцію деякої окружності, то його велика вісь завжди буде проекцією того діаметра окружності, який паралельний площині проекцій, а мала вісь еліпса буде являти собою проекцію діаметра, перпендикулярного йому. Внаслідок цього велика вісь еліпса проекції завжди дорівнює діаметру проецируемой окружності. Тут діаметр окружності CD перпендикулярний площині Н і проектується без спотворення на фронтальну площину. Для знаходження решт великий осі еліпса необхідно відкласти вниз і вгору від центру про 1 еліпса (по перпендикуляру до прямої о? О? 1) відрізки о? 1 ��? і про? 1 d? , Які дорівнюють половині діаметра окружності перетину о? 1 ��? = О? 1 d? = 1/2 (ab). При цьому діаметр АВ окружності паралельний горизонтальній площині, а його фронтальна проекція а? B? являє собою малу вісь розглянутого еліпса.

Точки, що відокремлюють видиму частину еліпса від невидимої. Почнемо з проведення фронтальній площині Q, яка ділить куля навпіл. Площина Q буде перетинати поверхню кулі по колу, проецирующейся на фронтальну площину у вигляді контуру. Тоді частина лінії перетину, розташовану на передній частині кулі, буде видно, якщо дивитися на кулю спереду, а інша її частина не буде видно. Площина Q перетне площину Р по фронталі Ф 1. Перетинаючись з контуром, її фронтальна проекція Ф визначить точки 1, які відокремлюють видиму частину кривої від невидимої. Проміжні точки 2? еліпса можна знайти за допомогою допоміжної фронтальній площині R, що перетинає поверхню кулі по колу радіуса r 2, а площину Р - по фронталі Ф2.

4. Косі перетину

Нехай потрібно побудувати натуральний вигляд перерізу фронтально-проектує площиною тіла. На малюнку 110а розглядається тіло, обмежене трьома циліндричними поверхнями (1, 3 і 6), поверхнею конуса (7) і сферою (5). При цьому циліндри 1 і 6 обмежені зверху площиною 8, а циліндр 3 обмежений з двох сторін площинами 2 і 4. Отже, крім кривих поверхонь, тіло також обмежена трьома площинами (2, 4 і 8), причому площину 8 не зачіпається січною площиною.

На малюнку 110б показана фронтальна проекція перетину, яка збігається зі слідом площини. Побудуємо натуральну величину перерізу, обмежуючись лише однієї його половиною.

Побудова роблять наступним чином:

1) циліндр 1 перетинається січною площиною по дузі еліпса, велика піввісь якого є без спотворення на головному вигляді a? F? . Тут центр еліпса розташовується на осі симетрії головного виду (точка f?), А відрізок FG є малою полуосью еліпса, яка дорівнює радіусу кола розглянутого циліндра 1.

Для дуги цього еліпса в перерізі ми будували чотири точки: А - кінець великої осі (вершина еліпса), G - кінець малої осі, С - проміжна точка і К - точка, в якій закінчується дуга еліпса;

2) лінія перетину в точці К переходить з поверхні циліндра 1 на верхню підставу циліндра 3 (на площину 2).

Відрізок KL прямий, по якій січна площина перетне площину 2, зображена в натуральну величину на плані (KL = kl);

3) від точки L до точки R ми маємо в своєму розпорядженні невеликий дугою еліпса, яка відповідає перетину з бічною поверхнею циліндра 3;

4) потім перетин проходить по прямій RN, яка належить площині 4 (RN = rn);

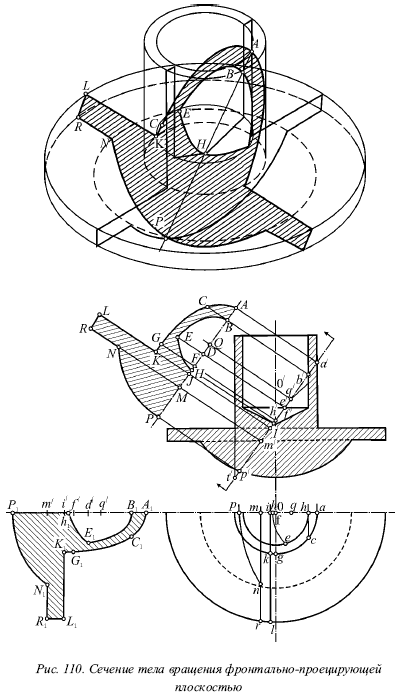
5) далі з площини 4 лінія перетину переходить на поверхню кулі 5, центр якого знаходиться в точці О, а центр кола, по якій січна площина перетинає поверхню кулі, 1 в точці Q. При цьому радіус цього кола дорівнює q? P? = QP, їм потрібно провести дугу з центру Q до зустрічі з прямою RM в точці N (MN = mn);

6) відповідно від перетину січної площини з поверхнею циліндра 6 повинна вийти дуга еліпса BE. Тут циліндри 1 і 6 мають загальну вісь, внаслідок чого у обох еліпсів один і той же центр знаходиться в точці F;

7) лінія перетину переходить в точці Е на поверхню конуса 7, тоді нахил січної площини по відношенню до основи конуса виявляється більше нахилу твірної. Отже, ми отримуємо гіперболу з вершиною в точці Н, а зліва від горизонтальної проекції на малюнку 110 побудований натуральний вигляд цього перетину.